deber

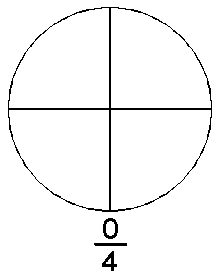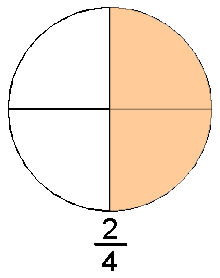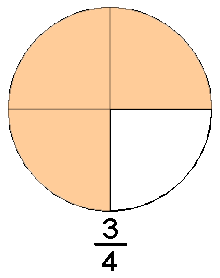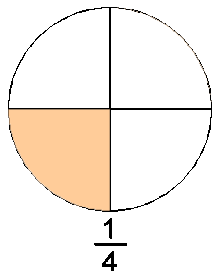
Números racionales

Número racional

Representación gráfica de las fracciones cuyo divisor es 4. Estas cuatro fracciones son números racionales.

Número racional es todo número que puede representarse como el cociente de dos números enteros o, más precisamente, un entero y un natural positivo;¹​ es decir, una fracción común ${\displaystyle a/b}$ con numerador ${\displaystyle a}$ y denominador ${\displaystyle b}$ distinto de cero. El término «racional» alude a una fracción o parte de un todo. El conjunto de los números racionales se denota por Q (o bien ${\displaystyle \mathbb {Q} }$, en negrita de pizarra) que deriva de «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los números enteros (${\displaystyle \mathbb {Z} }$), y es un subconjunto de los números reales (${\displaystyle \mathbb {R} }$).

La escritura decimal de un número racional es, o bien un número decimal finito, o bien periódico. Esto es cierto no solo para números escritos en base 10 (sistema decimal); también lo es en base binaria, hexadecimal o cualquier otra base entera. Recíprocamente, todo número que admite una expansión finita o periódica (en cualquier base entera) es un número racional.

}

     Has clic para jugar con Números racionales https://anagarciaazcarate.wordpress.com/category/numeros/fracciones/

Jerarquía de las operaciones con potencias y raíces

Jerarquia de las operaciones

1. 1. Jerarquía de lasoperaciones
2. 2. En matemáticas debemos respetar un orden y este orden es universal.Empecemos con un ejemplo, calcula el resultado de la siguiente cuenta: 2 + 5 x 7 =¿Qué resultado obtuviste?Si el resultado que llegaste fue 49, hay algo que no anda bien, veamos por qué.De acuerdo con el orden de las operaciones tiene prioridad las multiplicaciones, esdecir que primero resolveremos 5 x 7 que es 35 y luego le sumamos 2 y obtenemoscomo resultado 37.2 + 5 x 7 =2 + 35 = 37
3. 3. ¿Cómo es el orden de las operaciones?1. Resolver todos los cálculos de agrupación como paréntesis, corchetes y llaves.2. Resolver potencias y raíces.3. Multiplicar y dividir de izquierda a derecha.4. Sumar y restar de izquierda a derecha.
4. 4. Veamos algunos ejemplosresueltos…
5. 5. Ejemplo 1:38: 2 – 20 + 4 x 2 =En este ejemplo tenemos una división, una resta, una suma y una multiplicación.Si recordamos lo expuesto anteriormente debes respetar el orden de lasoperaciones, es decir primero debemos resolver la división y la multiplicación yaque éstas tienen la misma jerarquía es decir:38 : 2 – 20 + 4 x 2 =19 – 20 + 8 =Ahora sumamos y restamos de izquierda a derecha ya éstas también tienen elmismo orden de jerarquía19 – 20 + 8 = 7
6. 6. Ejemplo 2:Aquí comenzamos resolviendo la potencia y la raíz cuadrada por que ambastienen la misma jerarquía.Continuamos con la multiplicación y obtenemos:Y por último sumamos y restamos de izquierda a derecha y el resultado final es4434796237336347962127336
7. 7. Ejemplo 3:En este ejemplo tenemos un paréntesis, por lo tanto debemos comenzarresolviendo lo que se encuentra dentro de éste, pero para ello debemos respetarel orden de las jerarquías, es decir que primero resolveremos la potencia:50 – ( 4² + 120) =50 – ( 16 + 120) =Ahora si continuamos con el paréntesis sumando de izquierda a derecha y porúltimo restamos teniendo en cuenta la resta con números enteros:50 – 136 = - 86120450 2
8. 8. Ejemplo 4:Primero resolvemos lo que se encuentra dentro del paréntesis, es decir copiamos toda laoperación hasta llegar a este signo de colección y se coloca el resultado:12 – {-2 + 3. [4 – 4 + 1²] – 2} + 3 =Luego se resuelve la potencia que aparece:12 – {-2 + 3.[4 – 4 + 1] -2} + 3 =A continuación se resuelve la operación que encierra los corchetes:12 – {-2 + 3. 1 – 2} + 3 =Luego dentro de la llave se utiliza el orden de las operaciones, por lo que lo primero quese debe resolver es la multiplicación:12 – {-2 + 3 – 2} + 3 =Luego se resuelve la cuenta que quedo encerrada por las llaves:12 – (-4) + 3 =Por último, se saca la cuenta final:12 + 4 + 3 = 1932112843212 2
9. 9. Situaciones donde se aplican lasoperaciones combinadas
10. 10. Pedro se fue al centro de compras, gastó en la librería $25. Después fue a una tienda y quisocomprar 3 metros de una tela que valía $9 el metro, pero le faltaban $6.a) ¿Cuánto dinero tenía Pedro antes de entrar a la librería?b) ¿Cuál o cuáles de las siguientes expresiones permite resolver la situación anterior?Marcá con una X.A. (25+9) . 3 – 6B. 25 – (9.3 – 6)C. 25 + 9.3 – 6D. 25 + 9 : 3 - 6La respuesta correcta es la C.Ejemplo 1:
11. 11. Un grupo de chicos organizó rifas para comprar algunos equipos para la escuela. Quieren comprar untelevisor que cuesta $1.780, cuatro proyectores que cuestan $4.299 cada uno y 6 equipos de músicaque cuestan $479 cada uno. El dueño de una librería les ofreció regalarles los talonarios para las rifas.Escribí el cálculo que permita hallar el dinero total que tienen que recaudar.Solución:Ejemplo 2:47962994478

Has clic para jugar con Jerarquía de las operaciones con potencias y raíces https://anagarciaazcarate.wordpress.com/2014/05/25/bingo-de-potencias-y-raices/

Raiz cuadrada

Raíz cuadrada 

En matemática, la raíz cuadrada de un número x, es el número y que al ser multiplicado por sí mismo — elevarlo al cuadrado — resulta en x nuevamente, por tanto y²=x sería una ecuación equivalente.¹​ Es la radicación de índice 2 o, equivalentemente, la potenciación con exponente ¹⁄₂.

Cualquier número real no negativo x tiene una única raíz cuadrada no negativa, llamada raíz cuadrada principal y denotada como ${\displaystyle {\sqrt {x}}}$ donde ${\displaystyle {\sqrt {\ }}}$ es el símbolo raíz y x es el radicando.

Todo número real positivo tiene dos raíces cuadradas opuestas, ${\displaystyle {\sqrt {x}}}$, que es positiva, y ${\displaystyle -{\sqrt {x}}}$, que es negativa. Suelen denotarse de manera conjunta como ${\displaystyle \pm {\sqrt {x}}}$. Puesto que una de las dos se tiene que tomar como principal, la designación raíz cuadrada se refiere a la raíz cuadrada principal.

El concepto de raíz cuadrada puede extenderse a cualquier anillo algebraico, así es posible definir la raíz cuadrada de un número real negativo o la raíz cuadrada de algunas matrices. En los números cuaterniónicos los reales negativos admiten un número infinito de raíces cuadradas, sin embargo el resto de cuaterniones diferentes de cero admiten solo dos raíces cuadradas. En el anillo no conmutativo de las funciones reales de variable real con la adición y la composición de funciones si fºf = g, se puede plantear que f es la "raíz cuadrada" de g.²

Has clic para jugar con rais cuadrada http://www.mundoprimaria.com/juegos-matematicas/juego-raices-cuadradas/

Potencias de base entera y exponente natural

Potencias de base entera y exponente natura

Una potencia es un producto de factores iguales. Está formada por la base y el exponente.

	Exponente	Se puede leer: tres elevado a cuatro o bien tres elevado a la cuarta
3 . 3 . 3 . 3 = 3 4
	Base

El factor que se repite se llama base. El número de veces que se repite el factor, o sea la base, se llama exponente. Esto significa que si se tiene la potencia 2 6 (dos elevado a seis o a la sexta), la base será 2 y el exponente 6, lo cual dará como resultado 64 porque el 2 se multiplica por si mismo 6 veces (2 · 2 · 2 · 2 · 2 · 2 = 64).

Ejemplos:

2 5 =  2 • 2 • 2 • 2 • 2 =  32    El exponente es 5, esto  significa que la base, el 2, se debe multiplicar por sí misma cinco veces.

3 2 = 3 • 3 =  9                      El exponente es 2, esto significa que la base (3) se debe multiplicar por sí misma dos veces.

5 4 =  5 • 5 • 5 • 5  =  625       El exponente es 4, esto significa que la base (5) se debe multiplicar por sí misma cuatro veces.

Una potencia puede representarse en forma general como:

a n =  a • a • a • ........

Donde: a = base     n = exponente “ n” factores iguales

Finalmente, recuerda que una de las aplicaciones de las potencias es la descomposición factorial de un número.

Has clic para jugar con Potencias de base entera y exponente natural http://laescuelaencasa.com/matematicas-2/los-numeros-enteros/clase-20-potencias-de-base-entera-y-exponente-natual/

Operaciones combinadas con números enteros

Operaciones combinadas con números enteros


 Comenzando por la izquierda, vamos efectuando las operaciones según aparecen.

Ejemplo:

9 − 7 + 5 + 2 − 6 + 8 − 4 = 7

1.2 Combinación de sumas, restas y productos:

Realizamos primero los productos por tener mayor prioridad.

Posteriormente efectuamos las sumas y restas.

Ejemplo:

3 · 2 − 5 + 4 · 3 − 8 + 5 · 2 =
= 6 − 5 + 12 − 8 + 10 = 15

1.3 Combinación de sumas, restas, productos y divisiones:

Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.

Efectuamos las sumas y restas.

Ejemplo:

10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2 − 16 : 4 =
= 5 + 15 + 4 − 10 − 8 + 8 − 4 = 10

1.4 Combinación de sumas, restas, productos , divisiones y potencias:

Realizamos en primer lugar las potencias por tener mayor prioridad.

Seguimos con los productos y cocientes.

Efectuamos las sumas y restas.

Ejemplo:

2³ + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2² − 16 : 4 =
= 8 + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 4 − 16 =
= 8 + 5 + 15 + 4 − 10 − 8 + 16 − 4 = 26

Ejemplo de operaciones combinadas

12 − {7 + 4 · 3 − [(−2)² · 2 − 6)]}+ (2² + 6 − 5 · 3) + 3 − (5 − 2³ : 2) =

1 Primero operamos con las potencias, productos y cocientes de los paréntesis.

Ejemplo:

= 12 − [7 + 4 · 3 −(4 · 2 − 6)] + (4 + 6 − 5 · 3) + 3 − (5 − 8 : 2) =

2 Operamos con los productos y cocientes de los paréntesis.

Ejemplo:

= 12 − [7 +12 − (8 − 6)] + (4 + 6 − 15) + 3 − (5 − 4) =










has clic para jugar Operaciones combinadas con números enteros

matematicas

matematicas

matematicas

matematicas

matematicas

matematicas

Ecuaciones con estructura multiplicativa

Ecuaciones con estructura multiplicativa 

Para resolver una ecuación multiplicativa de primer grado o lineal se aplica el mismo procedimiento  que se  utilizan en las ecuaciones aditivas, la unica diferencia es que tenemos un número o coeficiente que multiplica la incognita.Otra diferencia es que devemos agrupar la x en uno de los miembros y los terminos conocidos en otro. 


     














Ecuaciones con estructura multiplicativa juegar https://es.scribd.com/doc/14500872/Ecuaciones-multiplicativas



   

Divisiones exactas de números enteros

Divisiones exactas de números enteros

Todo numero dividido para 1, da como resultado el mismo numero. Distributiva: Si el dividendo es suma o resta, se puede dividir por separado cada termino por el divisor y finalmente se realiza la suma o resta. 

Divisiones exactas de numeros enteros juega https://anagarciaazcarate.wordpress.com/category/numeros/enteros/